算数重要単元別の一覧> 平面図形の問題一覧 > 円とおうぎ形
◆著作権は中学受験の算数・理科ヘクトパスカルに帰属します。転載または、商用での無断使用を禁止します。
◆予習シリーズ手書き風解説のお申し込みページ(STORESに委託)
<円とおうぎ形-1>
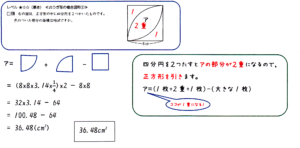
■右の図は,正方形の中に四分円を2つかいたものです。色のついた部分の面積は何C㎡ですか。
<円とおうぎ形-2>
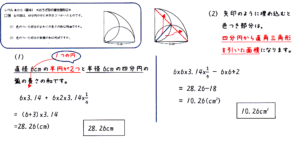
■右の図は,四分円の中に半円を2つかいたものです。
(1)色のっいた部分のまわりの長さの和は何cmですか。
(2)色のっいた部分の面積の和は何cniですか。
<円とおうぎ形-3>
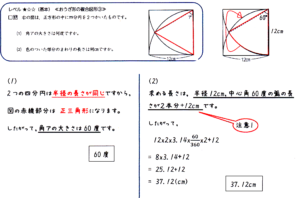
■右の図は,正方形の中に四分円を2つかいたものです。
(1) 角アの大きさは何度ですか。
(2) 色のついた部分のまわりの長さは何cmですか。
<目玉の問題の応用>
■右の図の四角形ABCDとPQRSは正方形です。辺ABの長さは10cmです。円周率は3.14とします。
(1)正方形PQRSの面積は何cm2ですか。
(2)かげをつけた部分の面積の和は何cm2ですか。
<解説ファイル>
<円とおうぎ形 面積 やや難>
■右の図のように直径が重なった 2つの半円があ ります。小さい半円の中心はAで ,半径は 30cm, 大きい半円の中心はBで ,半径は40cmです。この とき,斜線の部分の面積の和は何cm2ですか。ただ し,円周率は 3.14と します。
<解説ファイル>
<円とおうぎ形 面積>
■(図1)は,1辺が8cmの正方形ABcDの中に円をかぎその円に正方形EFGHをかいたものです。ただし,円周率は3.14とします。
(1) 正方形EFGHの面積は何cm2ですか。
(2) かげをつけた部分の面積は何cm2ですか。
■ 図2)は,半径6cmの半円です。かげをつけた部分の面積は何cm2ですか。ただし,円周率は3.14とします。
<解説ファイル>
<移動範囲の問題>
■右の図のように,たで2m,横4mの長方形の小屋があります。小屋のすみに4mのロープで犬がつながれています。小屋の外で犬が動ける範囲の面積は何cm2ですか。
ただし,円周率は3.14とします。
<解説ファイル>
<移動範囲の問題>
■右の図のような,台形ABCDがあります。ただし,円周率は3.14とします。
(1) 台形ABCDの面積は何cm2ですか。
(2) Aに10cmのひもをつけて,そのはしをPとします。Pが動くことができる部分の図形の面積は何cm2ですか。ただし,ひもは台形の中には入りません。
<解説ファイル>
<おうぎ形の分割>
図のP,Q は半径が 24 cmの四分円の弧ABを3等分した点です。斜線の部分の面積は何cm2ですか。ただし,円周率は3. 14とします。
<解説ファイル>


